The surprisingly complicated physics of why cats always land on their feet

Scientists are not immune to the alluringly aloof charms of the domestic cat. Sure, Erwin Schrödinger could be accused of animal cruelty for his famous thought experiment, but Edwin Hubble had a cat named Copernicus, who sprawled across the papers on the astronomer’s desk as he worked, purring contentedly. A Siamese cat named Chester was even listed as co-author (F.D.C. Willard) with physicist Jack H. Hetherington on a low-temperature physics paper in 1975, published in Physical Review Letters. So perhaps it’s not surprising that there is a long, rich history, spanning some 300 years, of scientists pondering the mystery of how a falling cat somehow always manages to land on their feet, a phenomenon known as “cat-turning.”

“The falling cat is often sort of a sideline area in research,” physicist and cat lover Greg Gbur told Ars. “Cats have a reputation for being mischievous and well-represented in the history. The cats just sort of pop in where you least expect them. They manage to cause a lot of trouble in the history of science, as well as in my personal science. I often say that cats are cleverer than we think, but less clever than they think.” A professor at the University of North Carolina, Chapel Hill, Gbur gives a lively, entertaining account of that history in his recent book, Falling Felines and Fundamental Physics.

Over the centuries, scientists offered four distinct hypotheses to explain the phenomenon. There is the original “tuck and turn” model, in which the cat pulls in one set of paws so it can rotate different sections of its body. Nineteenth century physicist James Clerk Maxwell offered a “falling figure skater” explanation, whereby the cat tweaks its angular momentum by pulling in or extending its paws as needed. Then there is the “bend and twist” (not to be confused with the “bend and snap” maneuver immortalized in the 2001 comedy Legally Blonde), in which the cat bends at the waist to counter-rotate the two segments of its body. Finally, there is the “propeller tail,” in which the cat can reverse its body’s rotation by rotating its tail in one direction like a propeller. A cat most likely employs some aspects of all these as it falls, according to Gbur.

Gbur is quick to offer a cautionary word of advice to anyone considering their own feline experiments: “Please don’t drop your cats!”—even in the name of science. Ars sat down with Gbur to learn more about this surprisingly prolific area of research.

Ars Technica: What led you to write an entire book about the physics of falling cats?

Greg Gbur: It really started with my love of the history of science and writing about it on my blog. One day, I was browsing old science journals, and I came across an 1894 paper about photographs of a falling cat landing on his feet. I wrote a blog post about it. But I wasn’t completely satisfied with the explanation, and I realized there were more papers on the subject. Every time I did a search, I found another paper offering another angle on the problem. Even in the last few weeks of writing the book, I still kept coming across minor little papers that gave me a little bit of a different take on the history.  It was surprising just how many papers there were about the falling cat problem. The more you look, the more you find people intrigued by how a cat lands on his feet. It seems like a problem that would be readily solvable.

Ars: Surely one of the issues was that photography hadn’t been invented yet, particularly high-speed photography. 

Gbur: Yes. Maxwell did his own preliminary investigations of the subject, but he pointed out that when you drop a cat from roughly two feet, it can still land on its feet, even if you’re dropping it upside down. That’s a really short period of time. The human eye simply can’t resolve that. So it was a problem that was largely not solvable until the technology was there to do high speed photography.

Étienne-Jules Marey did the first high speed photographs of falling down. It was almost an afterthought for him. He was doing all these different high-speed photographs of different animals, because that was his research, studying living creatures in motion. He presented the images of a falling cat, and it genuinely shocked the scientific community. One of the members at the meeting where the photographs were presented, said (and I paraphrase), “This young Marey has presented us with a problem that seems to go against the known laws of physics.”

The motions that are depicted in the photographs are quite complicated. The explanation given is part of the truth, but it seemed incomplete. It was good enough to convince physicists that a cat wasn’t violating the laws of physics, but it wasn’t good enough to convince everyone that it was the right explanation, or the complete explanation.

Ars: You summarize four distinct hypotheses offered at various times to explain the phenomenon of cat turning. So what is the best explanation we have so far for how a cat can turn and fall and land on its feet?

Gbur: This is part of why it was such a challenge: all these different motions play a role. If you’re looking at a series of photographs or a video of a falling cat, it becomes almost a psychological problem. Different people, their attention is going to be drawn by different aspects of a motion. But the most important is a bend and twist motion. The cat bends at the waist and counter rotates the upper and lower halves of its body in order to cancel those motions out. When one goes through the math, that seems to be the most fundamental aspect of how a cat turns over. But there are all these little corrections on top of that: using the tail, or using the paws for additional leverage, also play a role. So the fundamental explanation comes down to essentially bend and twist, but then there’s all these extra little corrections to it.

Ars: After all these studies, do we now know know exactly what’s going on with a falling cat, or is this still an area of active research?

Gbur: I don’t know that there’s anybody actively studying the cat model to try and get the finer details. It’s reached a point where understanding how a cat does it has reached, as a 19th century physicist once said, “hunting for higher decimal places.” Part of the catch is that every cat may do things just a little bit differently, because they are living creatures. You have heavier cats and lighter cats. I’ve got varieties of both at home. Longer cats and shorter cats. Each of them may twist and bend and tuck and turn just a little bit differently.

If you watch videos of falling cats, you will see that a lot of them use their tails to turn over. But we also know that cats without tails can turn over just fine. So from a physics point of view, the problem has reached a level where the details depend on the specific cat. People will still argue about it. I think a lot of physicists don’t realize how complicated the problem is, and they’re often just looking for a single simple solution. Physicists have an instinct to look for simple solutions, but nature’s always looking for the most effective solution. And those two approaches are not always the same.

“From a physics point of view, the problem has reached a level where the details depend on the specific cat.”

The emphasis these days is in that robotics area. Can we actually make a robot that can flip over like this, in as effective a way as a cat can. You can design a robot that, if you drop it upside down, can land right side up, but a cat can flip over and land right side up regardless of how it started— whether it’s upside down, whether it’s spinning, whether it’s on its side. There’s a video clip of a cat leaping up to grab a toy and it ends up flipping partially end over end as it leaps. And it does multiple twists and nevertheless manages to still land on its feet. That’s the sort of thing that I don’t think anybody has managed to get a robot to do yet. “Hey, I’m just gonna throw this robot up in the air with any sort of spinning motion I want, and nevertheless, have it still land perfectly on its feet.”

Two different approaches to the falling cat problem intersect in robotics. You can use mechanical models to try and understand what a cat is doing, and then you can also use robotics to try and replicate the cat’s motion properly. One is an analysis problem, where you’re saying, “I want to understand what’s going on.” The second part is a synthesis problem where you say, “I’m going to try and make a machine that can accurately reproduce it.”

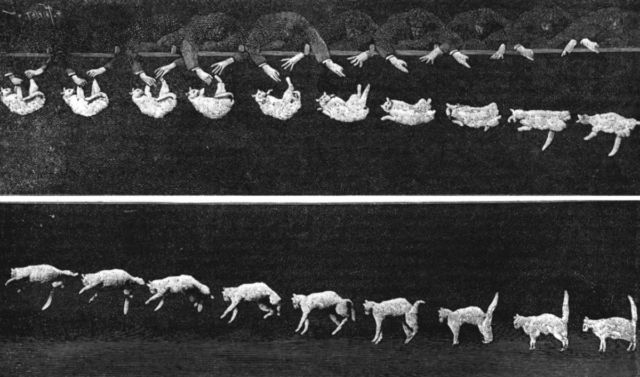
Ars: You also discuss a 2003 paper by physics philosopher Robert Batterman, in which he examines falling cats in terms of geometric phases, which in turn connects to a Foucault pendulum. Can you elaborate a bit on this particular connection?

Gbur: The basic idea is that there are a lot of physics problems where you can cycle the system. You start with the system and one condition, and you bring it through some change of behavior back to its original condition. But nevertheless it ends with a different behavior than it started. The falling cat is a good example. The cat starts upside down with his back straight, ends up right side up with his back straight. Even though it’s twisted and turned along the way, it ends up with a straight back again, but it’s now rotated 180 degrees.

Foucault’s pendulum is where you have this pendulum oscillating on the earth, a full day goes by, and the earth has done a full revolution. So the pendulum is spatially back where it started at the beginning of the previous day, but it is swinging in a different direction. The really remarkable thing is that the mathematics is structurally similar for all these different problems. So if you understand the falling cat problem, you understand a little bit about Foucault’s pendulum and how it works. Batterman also ties falling cats to polarized light and parallel parking as manifestations of the geometric phase in physics.

Ars: It sometimes seems like physicists don’t always appreciate how important their own history is to understanding current research.

Gbur: One reason I always emphasize learning a lot of science history is that it gives us a better understanding of how science is done. In basic physics classes, we’re often taught a very abbreviated and abridged version of the history, where you’re given the straight line path that leads to the end. I think of science history as sort of a maze. You’ve got a bunch of people wandering through this maze and a lot of people hit dead ends. That’s very natural, because nobody knows what they’re looking for. When we’re taught the history of science in class, we’re often only taught about the person who made it to the end of the maze without making any mistakes.

For students, that can give a very false impression that science is always about, “Yes, I know exactly what I’m doing and I know exactly where I’m going.” That isn’t the case. For the general public, it’s often useful to realize that, yes, science is always moving forward, but there are these dead ends, there are these mistakes along the way. It’s not perfect. That is not a condemnation of science, but the natural way things work.

https://arstechnica.com/?p=1636625