COVID-19 has claimed the life of Princeton mathematician John Conway. He was 82 years old.

The British-born Conway spent the early part of his career at Cambridge before moving to Princeton University in the 1980s. He made contributions in various areas of mathematics but is best known for his invention of Conway’s Game of Life, a cellular automaton in which simple rules give rise to surprisingly complex behaviors. It was made famous by a 1970 Scientific American article and has had a lively community around it ever since then. (Don’t confuse it with Milton Bradley’s board game of the same name.)

Conway’s Game of Life is played on a two-dimensional plane with square cells. Each square can be either black (“alive”) or white (“dead”). Simple deterministic rules dictate how the state of the board in one step leads to the next step. If a live square has two or three live neighbors (counting diagonals), it stays alive. If a dead cell has three live neighbors, it switches to black and becomes alive. Otherwise, the cell becomes—or stays—dead.

Conway developed these rules in the late 1960s, before the invention of the personal computer. He performed early experiments on a Go board and discovered that these rules could produce surprisingly complex behaviors. Before long, people were writing software to accelerate runs of the Game of Life.

One of the first non-trivial structures to be discovered was the glider, a five-square structure that moves diagonally across the board. People soon discovered that a wide range of these moving structures, dubbed spaceships, were possible. Spaceships could be of different sizes and move at different rates. They could also move in a number of different directions: vertically, horizontally, diagonally, and even at other angles.

In 1970, mathematician Bill Gosper discovered the first glider gun, a Game of Life structure that generates an infinite stream of gliders. Go enthusiasts found a variety of other guns, and they also found other examples of structures that emit other structures.

Puffers move across the Go board and leave behind chaos that congeals into static debris. Rakes move across the board emitting a stream of spaceships. Breeders leave a trail of guns behind them, with each gun generating a stream of gliders or other spaceships.

These structures can become unbelievably complex. This video, for example, shows a gun that consists of several large structures that each generates irregular streams of gliders. A bunch of gliders—37 to be exact—collide with one another in just the right way to produce a complex spaceship called a 6-engine cordership, which then proceeds in another direction. It takes 784 moves to produce a cordership before the cycle repeats.

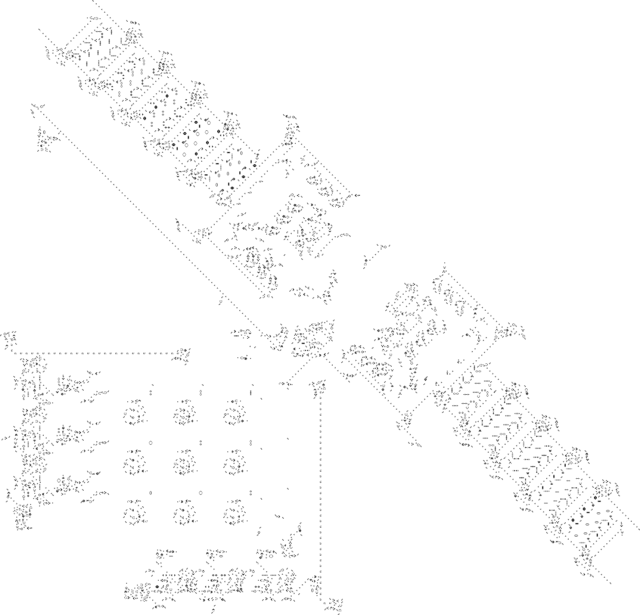
These elements, in turn, can become building blocks for still more complex structures. Mathematicians have demonstrated that it is possible to construct a Turing Machine on a Game of Life board. The Church-Turing thesis tells us that a Turing machine is theoretically capable of computing any function we can compute on modern computers—at least given enough time and storage space. So it’s theoretically possible, if not particularly efficient, to compute any function using the right arrangement of Game of Life cells.

More than 50 years after Conway invented the Game of Life, it continues to have an active community of both professional mathematicians and amateurs. The Conwaylife.com website has an extensive Wiki documenting hundreds of interesting Game of Life patterns. Game of Life enthusiasts have made thousands of posts at the site’s forums.

If you’d like to try out Conway’s Game of Life, it’s easy to do. There’s a solid Web-based game of life implementation here that will let you experiment with basic patterns. If you want to go deeper, you’ll likely want to download one of the many Game of Life software packages that are freely available online.

https://arstechnica.com/?p=1668004