I am a great believer in solving problems with lasers. Are you suffering from a severely polarized society and a fast-growing population living below the poverty line? Well, I have the laser to solve all your problems.

OK, maybe not. But when it comes to quantum computing, I believe that lasers are the future. I suspect that the current architectures are akin to the Colossus or the ENIAC: they are breakthroughs in their own right, but they are not the future. My admittedly biased opinion is that the future is optical. A new paper provides my opinion some support, demonstrating solutions to a mind-boggling 10³⁰ problem space using a quantum optical system. Unfortunately, the support is a little more limited than I’d like, as it is a rather limited breakthrough.

Photons flipping coins

The researchers have demonstrated something called a Gaussian boson sampling system. This is essentially a device designed to solve a single type of problem. It’s based on devices called “beam splitters,” so let’s start with a closer look at how those work.

If you shine light on a mirror that is 50 percent reflective, called a beam splitter, then half the light will be transmitted and half reflected. If the light intensity is low enough that only a single photon is present, it is either reflected or transmitted with the same randomness as a fair coin toss. This is the idea behind a beam splitter, which can take an incoming stream of photons from a laser beam and divide it into two beams traveling in different directions.

A beam splitter at 45 degrees can be thought of as a four-port device (see picture). In that picture, you can see that if two identical photons are incident on the same beam splitter from two different ports, then the result is not entirely random. They will both exit the same port, though which port they exit is random.

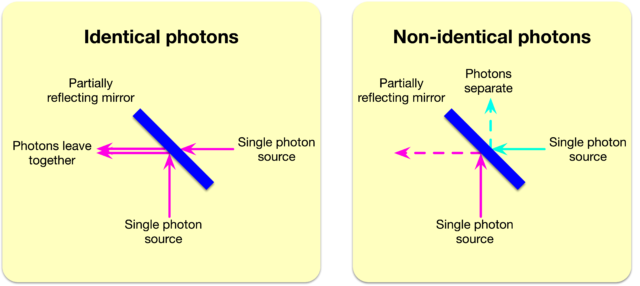
These two simple ideas, along with the idea of entanglement, result in a specific type of universal quantum computer, called a linear optical quantum computer. It’s basically a big network of beam splitters. Photons solve a problem by the way they spread through the network, which is determined based on where they exit.

Entanglement comes in the form of the path taken by the photons. Until and unless we measure that path, we cannot know its details, so we have to consider that all photons take all possible paths. Under these circumstances, if two photons arrive at a beam splitter at the same time via different ports, then their paths will become linked (entangled). Build a big-enough network of beam splitters and this can happen many times, creating sprawling entangled states.

Flipping entangled photonic coins

The number of output states scales very quickly with the number of inputs and beam splitters. In the current demonstration, the researchers used 50 inputs and—the exact type of device is not described—a chip with the equivalent of 300 beam splitters. The total number of possible output states is about 10³⁰, which is about 14 orders of magnitude greater than the next biggest demonstration of quantum computing.

Photons are sent into the network (one at each input) and exit in a state that is randomly chosen from all possible states. In less than four minutes, the researchers had obtained results that they estimate would take a fast classical computer about 2.5 billion years to calculate.

This was followed by careful tests to check that the behavior was indeed quantum. Now, of course, computing the exact output for a full input is impossible. But it is possible to calculate what would happen given specific input states and compare the output states with the results of those calculation. It is also possible to calculate the output of the network if the light is not in a quantum state or if the photons are not identical. In the first case, the measurement results match the predictions, and in the second two cases, the measurement results don’t match the predictions. This provides strong evidence for the result being due to quantum effects.

Flipping useless

In many respects, this is a fantastic result. I don’t think anyone can very easily argue that the researchers have not demonstrated a quantum speed-up. It is also an incredible engineering achievement. One laser provides 25 equal-intensity beams, each carefully aligned to two crystals that each generate single photons. These are then carefully aligned to optical fibers, the outputs of which have to be carefully coupled to the chip that houses the beam splitters. The outputs need to be carefully aligned to photodetectors. The whole setup, which probably occupies an area of about 1.5m x 2.5m, has to be carefully stabilized to high precision (about 10nm). No doubt there are several super-proud PhD students who did all of that painstaking work.

On the other hand, the work is no different to other quantum-advantage experiments: take a problem that is mostly useless but happens to map exactly to the architecture of your computer. Naturally, the computer can solve it. But the point of a computer—and this is why the researchers do not refer to the device as a computer—is to solve many different useful problems. And for these cases, we have not yet seen undisputed evidence of the promised quantum advantage. I have no doubt that it will come, though.

Light is enlightening

Even though this work is not as overwhelmingly positive as it first seems, I still think optical quantum computers are the way to go.

At the moment, practical quantum computers come in only two flavors. The licorice-flavored variety consists of a string of ions (an atom with an electron removed) that are all lined up like a string of pearls. The ions are far enough apart that they can be separately addressed, which means that information (in the form of quantum bits, called qubits) can be stored and read from individual atoms. Computation operations can be performed using microwaves and by using the motion of the ions. Here, each bit is highly reliable, but performing complex computation is a rather difficult and stately dance of microwave pulses and laser pulses.

The lemon sherbet of quantum computers are the liquid-helium-cooled superconducting rings. Each ring represents a qubit, which are addressed and coupled to each other via wires. The advantage of this approach is that the hardware is relatively easy to scale—it’s basically the same skill as making printed circuit boards. But the quantum behavior of each qubit is much easier to disrupt, so your board is unlikely to work. You compensate for the reliability problem by repeating the computation many times and looking for the most common answer.

Neither option is particularly attractive in any context other than quantum computing as a service.

Size and temperature

Unlike both of these options, an optical quantum computer could be a (large) chip-scale device that is powered by an array of laser diodes, with readout done by a series of single-photon detectors. None of these require ultralow temperatures or vacuum (if photon-counting detectors are required, liquid nitrogen would be required). Optical quantum computing will require temperature stability and, as this paper demonstrates, a rather complicated feedback system to ensure that the lasers are working exactly as required. However, all of that could be contained in one large rack-mounted box. And that is, for me, the critical advantage of optical systems.

This does not mean that light will win, though. After all, germanium is a better semiconductor than silicon, but silicon still rules the roost.

Science Magazine, 2020, DOI: 10.1126/science.abe8770 (About DOIs)

https://arstechnica.com/?p=1727926