Sicurezza e matematica, ovvero quando la matematica viene in soccorso della sicurezza per renderla più efficiente in termini di tempo e più solida in termini di soluzioni. In particolare in questo articolo vedremo come la security utilizza l’SMT, Satisfiability Modulo Theories (Riquadro 1), in vari campi.

Gli SMT solver non sono uno strumento nuovo, così come non è innovativo il loro utilizzo nell’ambito della sicurezza. Una maggiore capacità dell’hardware e una migliore resa degli algoritmi che stanno dietro ai solver hanno reso le soluzioni che coniugano sicurezza e SMT ampiamente utilizzate e utili a risolvere problemi che fino a qualche tempo fa erano noiosi, quindi soggetti ad errore, o, peggio ancora, non facilmente risolvibili. Inoltre, la complessità delle nuove tecniche di offuscamento, ma anche del software in generale, ha reso necessario un nuovo tipo di tool e un nuovo tipo di operazioni di analisi.

I campi riconducibili alla sicurezza che fanno uso di un SMT solver possono essere ricondotti a tre grandi famiglie:

• Ricerca di bug
  • Fuzzing
  • Analisi
• Generazione di exploit
  • Generazione di exploit automatizzata
  • Proof of Concept
  • Generazione di payload automatizzata
• Malware Analysis
  • Obfuscation
  • Packing
  • Anti-debugging
  • Crittoanalisi

Vediamo in dettaglio come alcune di queste operazioni si avvalgono di un SMT solver.

Riquadro 1: breve introduzione a SMT e SAT

Non vedremo nel dettaglio gli SMT, ma ci basta sapere che questi strumenti funzionano e si basano su solide teorie matematiche.

In matematica una formula booleana (che ritorna i valori vero o falso) si dice soddisfacibile se esiste almeno un valore delle variabili per le quali quella formula è verificata. Per la soluzione sono possibili tre stati:

• La formula non può essere soddisfatta
• La formula può essere soddisfatta
• Risultato ignoto (possibile timeout)

Gli SMT si occupano proprio di questo: data una formula determinano il suo stato e, se esistono, i valori delle variabili che la verificano.

Gli SMT solver utilizzano dei SAT solver come backend: in pratica li possiamo vedere rispettivamente come linguaggio di alto livello e assembly, ovvero, i SAT solver sono molto più efficiente ma anche più complessi da programmare e manutenere.

Ricerca di bug

Symbolic execution e concolic execution

Senza scendere nei dettagli di queste analisi, che vedremo meglio in un prossimo articolo, vediamo ora come gli SMT solver intervengono in tali casi.

In una esecuzione concreta (figura 2) un’applicazione è eseguita con uno specifico set di input che eseguirà un unico path.

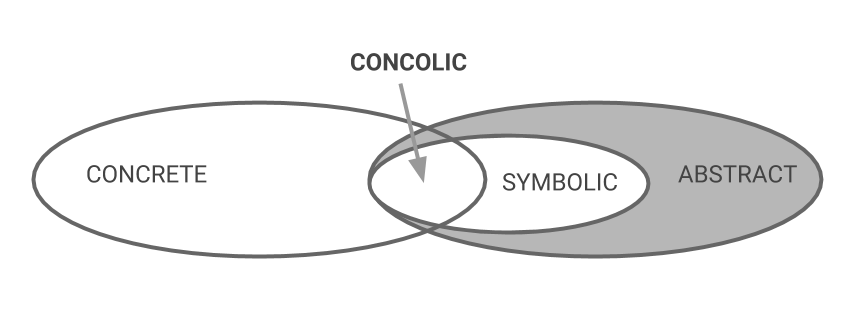
Invece, una symbolic execution, tecnica nata a metà degli anni ’70, consiste nell’analizzare un’applicazione determinando quali valori di ingresso causano l’esecuzione di un determinato percorso. Per fare ciò vengono assunti come input dei valori simbolici invece dei normali input dell’applicazione e viene quindi seguita l’esecuzione del programma.

L’esecuzione simbolica di un’applicazione può generare tutti i possibili percorsi che un programma può raggiungere durante un’esecuzione concreta in corrispondenza di determinati valori di input. Si capisce subito che, anche se dal punto di vista della copertura non c’è nessun problema, un simile approccio non è sostenibile in pratica.

Per ovviare a ciò si fa ricorso alla concolic execution (unione dei termini concrete e symbolic). Un approccio molto diffuso di concolic execution è la dynamic symbolic execution (DSE) dove l’esecuzione concreta è guidata da quella simbolica. In sostanza la concolic execution è una tecnica ibrida che si basa sulla symbolic execution, che è utilizzata insieme ad un automated theorem prover o ad un constraint solver per generare input concreti, allo scopo di massimizzare la copertura del codice.

Semplificando, un model checker, basato su un solver SMT, viene utilizzato per verificare se il path definito dal symbolic execution engine è realizzabile; ovvero se esistono dei valori concreti che soddisfano la formula definita dall’engine.

I principali framework che si occupano di esecuzione simbolica fanno largo uso dei solver SMT nelle loro procedure di analisi di un software (figura 3).

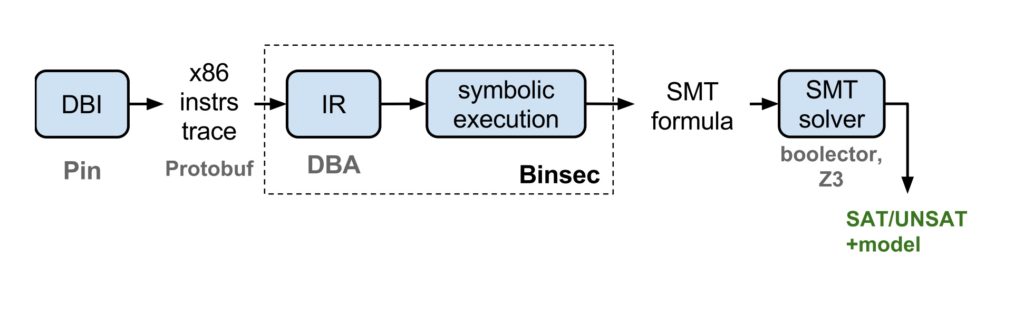
Però, come avviene per la symbolic execution, anche la concolic execution ha dei limiti. Nonostante il notevole sviluppo degli SMT solver, un’analisi basata sulla concolic execution di un’applicazione di media grandezza è impraticabile, quindi è possibile analizzare solo parti limitate dell’esecuzione. Inoltre, i solver attuali, anche i più evoluti, non garantiscono buone prestazioni quando si ha a che fare con un certo numero di variabili e condizioni.

Symbolic-Assisted Fuzzing

Si hanno quindi grossi limiti in termini di efficienza. Per poter sopperire a tale deficit si fa in genere uso dei fuzzer, utilizzando strumenti che generano valori casuali di input, in modo da portare l’applicazione esaminata a raggiungere stati inattesi. Anche questi strumenti presentano diversi limiti.

Ricapitolando, entrambe le tecniche utilizzate nella ricerca automatizzata di bug, concolic execution e fuzzing, presentano dei limiti per quanto riguarda la copertura del codice, però fortunatamente sono limiti complementari. Di conseguenza, è sempre più diffuso un processo ibrido che vede l’utilizzo allo stesso tempo di entrambe le tecniche.

Malware analysis

L’SMT ci torna utile quando abbiamo a che fare con l’elaborazione, di una o più variabili, riconducibile ad una formula matematica. Ad esempio, quando ci troviamo di fronte ad un assembly dove ci viene chiesto di determinare una chiave calcolata in vari passi con diverse operazioni e che ha questi vincoli:

• La chiave è formata da 3 valori interi: a, b e c
• a è multiplo di 5
• il risultato dell’or tra a e b è 123
• a > 0x12345678
• c è la media di a e b
• c è minore di 0x76543210

possiamo tradurre tutto in formule e usare un solver SMT per risolvere il problema. Usando il solver Z3, una delle tante implementazioni dell’SMT, (https://github.com/Z3Prover/z3) avremo:

from z3 import *

a = BitVec(‘a’, 32)
b = BitVec(‘b’, 32)
c = BitVec(‘c’, 32)

s = Solver()
s.add(a % 5 == 0)
s.add(((a | b) & 0xFF) == 123)
s.add(a > 0x12345678)
s.add(c == (a + b)/2)
s.add(c < 0x76543210)

if s.check():
print(s.model())

Come risultato avremo dei valori di a, b e c che verificano i vincoli. Ad esempio: [b = 2647883066, a = 556565315, c = 3749707839]

Malware obfuscation

I malware tipicamente fanno largo uso di packer e tecniche di offuscamento, in modo da rendere più ardua l’analisi.

Eseguite singolarmente le analisi statiche, dinamiche e simboliche non sono sufficienti ad analizzare in modo completo un malware del genere. Scopo finale di un’analisi è invertire la trasformazione, oppure, se questo non è possibile, almeno di rendere più agevoli le analisi successive, semplificando il codice: ovvero di fornire del codice disassemblato semanticamente esatto come definito dall’esecuzione simbolica.

In definitiva, l’equivalence checking, effettuato da un SMT solver, consiste nel valutare la correttezza di un’operazione di deoffuscamento; per la serie: è più difficile camuffare la semantica di un’applicazione invece che la sua forma sintattica.

Generazione di exploit

Quando dobbiamo trovare dei gadget utili ad un attacco di tipo ROP (https://www.ictsecuritymagazine.com/articoli/rop-cercare-gadget-nelle-applicazioni-android/), un SMT solver viene in aiuto essenzialmente in due casi: nella ricerca semantica dei gadget e in un compilatore ROP.

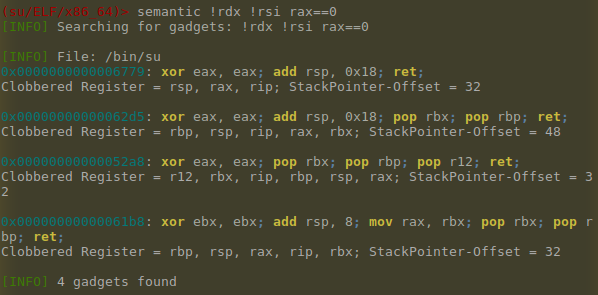
Nel primo caso, un solver trova tra tutti i gadget esistenti in un’applicazione quelli che sono funzionalmente equivalenti ad un determinato comportamento. In altre parole, cerca di trovare una equivalenza tra un singolo gadget e un modello definito in precedenza. Ad esempio, per implementare la ricerca semantica dei gadget, Ropper (https://github.com/sashs/Ropper) utilizza pyvex per creare una rappresentazione intermedia del software in esame e z3 come solver SMT:

(ropper)> help semantic
semantic  –  Searchs gadgets
semantic <constraint>[; <constraint>][ !<stable reg>*]

Example:
semantic eax==ebx; ecx==1 !edx !esi

Valid constraints:
reg==reg
reg==number
reg==[reg]
reg<+|-|*|/>=<reg|number|[reg]>

In Figura 4 è riportato un esempio di ricerca semantica: abbiamo cercato gadget che non modificano i registri RDX e RSI ma impostano RAX a zero.

Nel caso invece di un compilatore ROP, ovvero uno strumento capace di generare delle ROP chain, l’SMT aiuta a creare delle sequenze di gadget semanticamente simili ad un modello di payload.

Conclusioni

In questo articolo abbiamo visto solo alcune applicazioni dell’SMT nell’ambito della sicurezza. I campi di applicazione di questa tecnica, ma anche di altre mutuate dalla matematica, sono in continua evoluzione soprattutto nell’ambito del reverse engineering, disciplina legata a filo doppio alla matematica.

Articolo a cura di Gianluigi Spagnuolo

Si interessa di sicurezza informatica, reti di sensori e ingegneria del sotware.

Attualmente si occupa pricipalmente dell’analisi dei dati.

Collabora con diverse riviste del settore scrivendo di programmazione e sicurezza

https://www.ictsecuritymagazine.com/articoli/analisi-e-smt-satisfiability-modulo-theories/